Regression and Recognition in C
A little while ago, I thought it would be a fun task to try and perform two basic modes of supervised machine learning in C: linear regression and some basic image recognition. This is generally what followed, and the entirety of the code can be found at mufaro3/cml.
Linear Regression
For linear regression, I opted to use least-squares linear regression as solved by way of basic linear algebra. From Wikipedia [1], Least-squares linear regression in this form takes on the equation
\[\beta = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y} = \begin{pmatrix} b \\ m \end{pmatrix}\]where
\[\mathbf{X} = \begin{pmatrix} 1 & x_1 \\ 1 & x_2 \\ \dots & \dots \\ 1 & x_n \end{pmatrix}\]and
\[\mathbf{y} = \begin{pmatrix} y_1 \\ y_2 \\ \dots \\ y_n \end{pmatrix}.\]Thus, it was straightforward to write this process, but the hard part would be actually making my own linear algebra library. Thus, what I did was start from the top-down with the main function, where I used GNUPlot to display the results:
void
regression_example ()
{
const size_t size = 10;
double x[] = {1, 3, 4, 6, 7, 9, 11, 12, 14, 15};
double y[] = {4, 7, 9, 12, 14, 18, 20, 24, 27, 29};
RegressionResult result = calculate_linear_regression(x, y, size);
gnuplot_ctrl *fig = gnuplot_init();
...
}From there, I would write in the form described by
\[\beta = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y} = \begin{pmatrix} b \\ m \end{pmatrix}\]as
RegressionResult
calculate_linear_regression ( double *x, double *y, const size_t size )
{
Tensor2D *x_tensor = Tensor2D_load_xvalue_tensor ( x, size );
Tensor2D *y_tensor = Tensor2D_load_yvalue_tensor ( y, size );
...
/* intermediate steps
https://en.wikipedia.org/wiki/Linear_least_squares#Fitting_a_line */
Tensor2D *x_tensor_transposed = Tensor2D_transpose( x_tensor );
...
Tensor2D *x_gram = Tensor2D_mult( x_tensor_transposed, x_tensor );
...
Tensor2D *x_gram_inverse = Tensor2D_sq_inverse( x_gram );
...
Tensor2D *gram_inv_trans_prod = Tensor2D_mult( x_gram_inverse, x_tensor_transposed );
...
Tensor2D *beta = Tensor2D_mult( gram_inv_trans_prod, y_tensor );
...
/* obtain slope and intercept from beta */
double intercept = Tensor2D_get_index( beta, 0, 0 );
double slope = Tensor2D_get_index( beta, 1, 0 );
...
}(with a lot of debugging code and whatnot obviously omitted for brevity). From there, it was just a whole lot of writing this miniature linear algebra library, which largely consisted of me running back and forth between wikipedia articles and ChatGPT to figure out how to implement things like matrix inversion or multiplication and addition, and because this was generalized for matrices and vectors, I just called all the objects tensors for simplicity. That might be wrong mathematical description but I really don’t care.
By far, the hardest function to write in the linear algebra library was the matrix inversion function Tensor2D_sq_inverse, as the algorithm for calculating the Gauss-Jordan inverse via Gaussian elimination is notoriously complex.
/* TODO: fix the fact that the intermediate augment isnt modified, but the OG matrix is
by producing a copy of the OG at the beginning OR writing its values to the ia
then performing all operations DIRECTLY onto the ia inplace. */
Tensor2D *
Tensor2D_sq_inverse ( Tensor2D *t )
{
/* tensor must be square */
if (t->rows != t->cols)
return NULL;
/* copy t to a new tensor */
t = Tensor2D_copy( t );
/* gauss-jordan elimination to calculate the inverse
https://en.wikipedia.org/wiki/Gaussian_elimination */
Tensor2D *intermediate_augment = Tensor2D_create( t->rows, t->cols + t->rows );
Tensor2D *ia = intermediate_augment;
/* copy the data to intermediate augment */
for ( size_t r = 0; r < t->rows; ++r ) {
for ( size_t c = 0; c < t->cols; ++c )
Tensor2D_set_index( ia, r, c, Tensor2D_get_index( t, r, c ) );
/* set up the identity matrix */
Tensor2D_set_index( ia, r, r + t->rows, 1 );
}
fprintf(stderr, "INTERMEDIATE AUGMENT TENSOR BEFORE\n");
Tensor2D_print( intermediate_augment );
/* forward elimination */
for ( size_t pivot = 0; pivot < t->rows; ++pivot ) {
/* find the pivot row (with the largest abs value in the column) */
size_t max_row = pivot;
double max_val = fabs( Tensor2D_get_index( ia, pivot, pivot ) );
for ( size_t r = pivot + 1; r < t->rows; ++r ) {
double val = fabs( Tensor2D_get_index( ia, r, pivot ) );
if ( val > max_val ) {
max_val = val;
max_row = r;
}
}
/* matrix is singular */
if (max_val == 0) {
Tensor2D_destroy( &t );
Tensor2D_destroy( &ia );
return NULL;
}
/* swap pivot row */
Tensor2D_inplace_swap_rows( ia, pivot, max_row );
/* normalize pivot row */
Tensor2D_inplace_divide_row( ia, pivot, Tensor2D_get_index( ia, pivot, pivot ) );
/* eliminate other rows */
for (size_t r = 0; r < t->rows; ++r) {
if (r == pivot)
continue;
double factor = Tensor2D_get_index( ia, r, pivot );
for (size_t c = 0; c < ia->cols; ++c)
Tensor2D_set_index( ia, r, c,
Tensor2D_get_index( ia, r, c ) -
factor * Tensor2D_get_index( ia, pivot, c ) );
}
}
fprintf(stderr, "INTERMEDIATE AUGMENT TENSOR AFTER\n");
Tensor2D_print( intermediate_augment );
/* copy data */
Tensor2D *sq_inv_result = Tensor2D_create ( t->rows, t->cols );
for ( size_t r = 0; r < t->rows; ++r )
for ( size_t c = 0; c < t->cols; ++c )
Tensor2D_set_index ( sq_inv_result, r, c,
Tensor2D_get_index ( intermediate_augment, r, c + t->rows ) );
/* free intermediate and return */
Tensor2D_destroy( &t );
Tensor2D_destroy( &intermediate_augment );
return sq_inv_result;
}As you can see, it really was not fun to write, and I even still have debug prints all over the place and an unfinished TODO sitting at the top of the function. It’s a real mess. However, if it works, it works, so once it worked once, I called it a day.
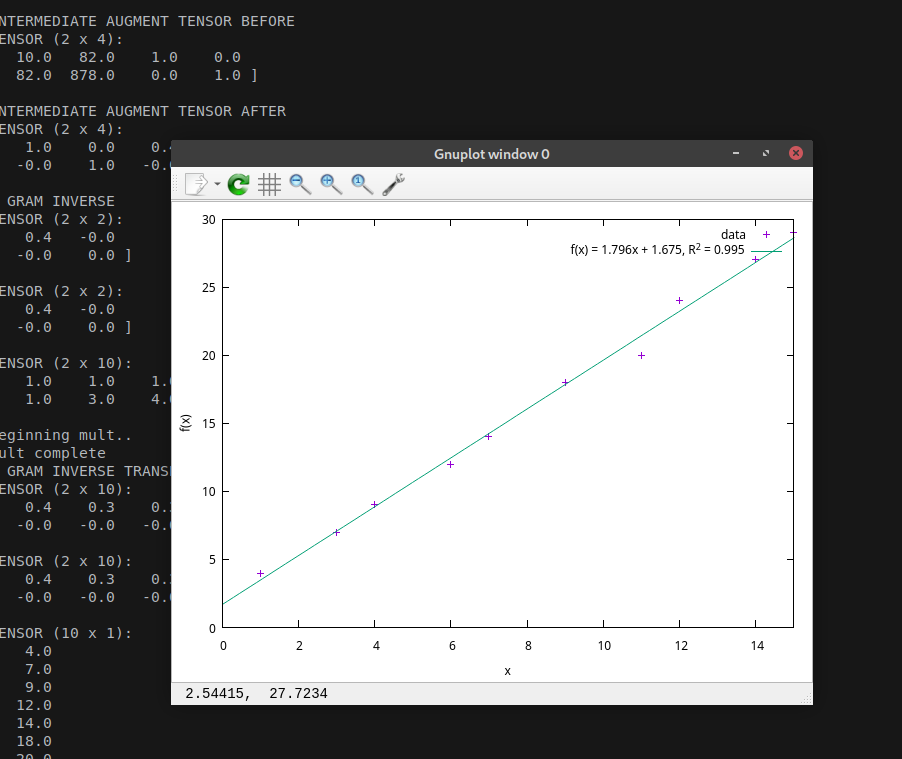
The final result! It worked!
This bit taught me quite a bit about writing mathematical code in C. It’s a hassle, but rewarding. The urge to use a library is always so strong, but if you resist and write your own, you’ll feel real proud.
Image Recognition
And now, for the real interesting part. Once I got the regression working, I felt like I could do anything, so then I went for image recognition, again without a library. I opted for CIFAR-10 to keep things as simple as possible, with the following main method:
void
classification_example ()
{
Dataset *cifar = dataset_load_cifar("./data/cifar-10");
...
Model *model = model_new ( cifar->image_size, cifar->num_classes, 0.001 );
model_train ( model, cifar, 10 );
...
model_test ( model, cifar );
model_save_to_file ( model, "cifar-10-model.bin" );
model_destroy ( &model );
dataset_close ( &cifar );
}The structure of the dataset and model were pretty simple, with the dataset essentially acting like a vector of batches of data, and each batch is like a vector of samples (where a sample is essentially just an image in CIFAR and its associated label):
typedef struct {
double *image;
size_t label, image_size;
} Sample;
typedef struct {
Sample **samples;
size_t num_samples;
} Batch;
typedef struct {
/* data */
Batch **test_batches, **train_batches;
size_t test_batches_len, train_batches_len;
/* dataset metadata */
size_t batch_size, image_size, num_classes;
char **label_map;
/* did the load fail */
bool failure;
} Dataset;Next, the model essentially just consists of two arrays of numbers, the weighs and biases of the model, alongside a struct for a prediction on a given sample, which is essentially just the output probability distribution across all ten classes:
typedef struct {
float *scores;
/* vector sizing */
size_t num_classes, most_likely;
/* for error handling */
bool failure;
} Prediction;
typedef struct {
double *weights, *biases;
size_t image_size, num_classes;
float learning_rate;
/* model metrics */
size_t *guess_dist;
size_t total_guesses;
} Model;Predictions for the model are produced using the weights and biases of the model
Prediction *
model_predict ( Model *model, Sample *sample )
{
static unsigned int debug_counter = 0;
float *scores_raw = calloc ( model->num_classes, sizeof(float) );
Prediction *pred = malloc ( sizeof(Prediction) );
pred->scores = calloc ( model->num_classes, sizeof(float) );
pred->num_classes = model->num_classes;
/* generate raw predictions (convert to a probability distribution) */
for (size_t ci = 0; ci < model->num_classes; ci++) {
scores_raw[ci] = model->biases[ci];
for (size_t k = 0; k < sample->image_size; k++)
scores_raw[ci] += model->weights[ci * model->image_size + k] * sample->image[k];
}
/* normalize via softmax */
softmax(scores_raw, pred->scores, model->num_classes);
/* determine the most likely from the highest score */
...
return pred;
}and normalized via the softmax function [2] in form
\[\sigma(\mathbf{z})_i = \frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}}\]void
softmax (float *input, float *output, size_t len)
{
float max_val = input[0];
for (size_t i = 1; i < len; i++)
if (input[i] > max_val)
max_val = input[i];
float sum = 0.0;
for (size_t i = 0; i < len; i++) {
output[i] = expf(input[i] - max_val);
sum += output[i];
}
for (size_t i = 0; i < len; i++)
output[i] /= sum;
}Let \(\mathbf{p}\) be the probability distribution and from a prediction and \(p_i\) be the probability of guess \(i\). Where \(h\) is the true label of the image, the error of the model at class \(i\) is defined as
\[R_i = \begin{cases} 1-p_i & \text{ if } i=h \\ p_i & \text{ elsewhere,} \end{cases}\]and the total error of the model on a prediction becomes
\[R = \sum_{i=1}^{10} R_i.\]From the error, the weights and biases can be updated accordingly based on the learning rate \(\ell\), with the bias \(b_i\) on class \(i\) and weight $k$ on pixel value \(k\) becoming
\[b_i := b_i - \ell R_i\]and
\[w_i := w_i - \ell R_i k\]void
model_train ( Model *model, Dataset *dataset, const size_t epochs )
{
for ( size_t epoch = 0; epoch < epochs; ++epoch ) {
double total_loss = 0;
...
for ( size_t batch_index = 0; batch_index < dataset->train_batches_len; ++batch_index ) {
Batch *batch = dataset->train_batches[batch_index];
for ( size_t sample_index = 0; sample_index < batch->num_samples; ++sample_index ) {
/* generate prediction */
Sample *sample = batch->samples[sample_index];
Prediction *pred = model_predict(model, sample);
...
/* compute losses and gradients */
for ( size_t class_index = 0; class_index < dataset->num_classes; ++class_index ) {
bool correct = class_index == sample->label;
double predicted = clamp( pred->scores[class_index], 1e-9, 1.0 - 1e-9 );
double error;
if ( correct ) {
error = -predicted;
total_loss += -log( predicted );
} else
error = predicted;
...
/* update weights and biases in the model */
for ( size_t k = 0; k < sample->image_size; ++k )
model->weights[ class_index * model->image_size + k ] -= \
model->learning_rate * error * sample->image[ k ];
model->biases[ class_index ] -= model->learning_rate * error;
}
...
}
}
...
}
}Now, in practice, my code entirely sucks. The model tends to guess correctly about 1/3 of the time, which is pretty bad, but to be expected for this situation. At least I was fairly proud of it!
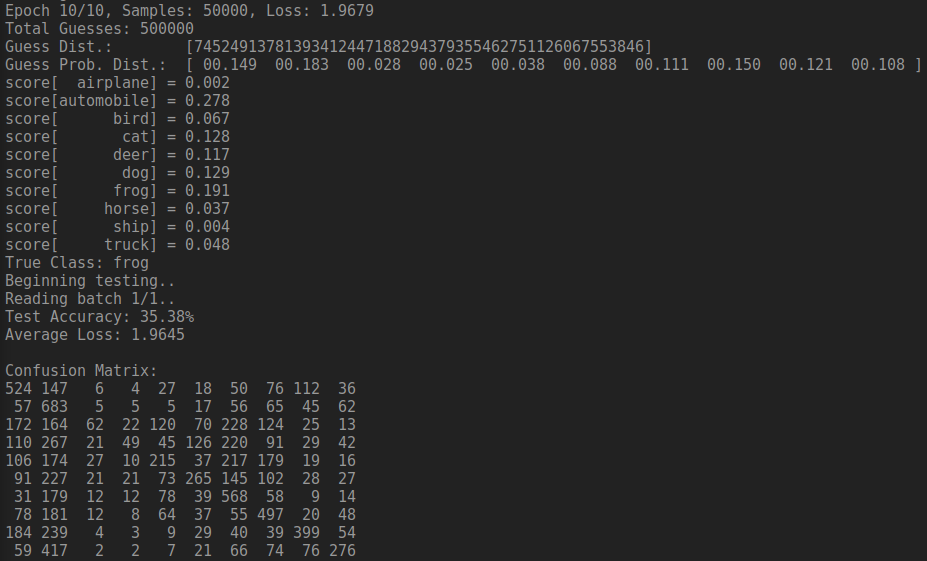
The classifier worked! Huzzah! Works cannot begin to explain how ecstatic I was to see it work even somewhat, despite only guessing correctly about 35% of the time.
[1] “Linear Least Squares” on Wikipedia. Link
[2] “Softmax Function” on Wikipedia. Link
If you like my posts, feel free to subscribe to my RSS Feed.